특정한 확률 분포를 따르는 난수 생성하기
Random Number Generation With A Specific Probability Distribution.
난수 생성은 여러가지 pseudo-random number generation 알고리즘으로 만들어진 다양한 라이브러리를 통해서 쉽게 할 수 있다. Python의 경우 NumPy의 random 패키지를 이용하면 균등한 확률분포를 따르는 난수와 정규분포를 따르는 난수 등을 생성할 수 있다. 그런데 이러한 라이브러리에 없는 확률분포를 따르는 난수를 생성해야할 경우가 있을 것인데, 이 경우에는 어떤 과정을 통해 원하는 난수를 얻을 수 있는지 살펴보자.
Uniform Sample
난수가 주어진 두 수 $a$, $b$사이의 값을 가지며 균일하게 분포하는 경우를 uniform sample이라 한다. 다음과 같이 Python의 NumPy 라이브러리를 이용하여 uniform한 난수를 얻을 수 있다.
import numpy as np
import matplotlib.pyplot as plt
# uniform sampling in range from 0 to 1, with 10000 samples
uniform_sample = np.random.rand(10000)
plt.figure()
plt.plot(uniform_sample, marker='.', ls='', c='k', ms=1)
plt.title('Uniform Sample')
plt.ylabel('u')

0과 1사이의 값을 가지는 uniform sample을 $u$라고 하자. 이 $u$가 0과 1사이의 값을 가지기 때문에, $u$를 어떤 값의 확률로 해석할 수 있을 것이다. 만약 어떠한 확률변수 $X$가 특정한 값 $x$보다 작을 확률 $P(-\infty \le X \le x)$을 $u$로 놓고, $u$값과 $X$의 확률분포로부터 $x$를 얻는 함수를 얻는다면, $X$의 확률분포를 따르는 난수 $x$를 $u$로부터 얻을 수 있다. 결과적으로 $u$로부터 $x$를 얻는 함수는
\begin{equation} x = F^{-1}(u) \end{equation}
\[F(x) = \int f(x)dx\] \[f(x) \text{는 } X\text{의 확률밀도함수}\]예를 들어, $P(X)$가 표준정규분포(normal distribution)라면 $u$값에 대응하는 $x$값은 다음과 같다.
| $u$ | \(y = F^{-1}(u)\) |
|---|---|
| 0.5 | 0 |
| 0.975 | 1.95996 |
| 0.995 | 2.5758 |
| 0.999999 | 4.75342 |
| $1-2^{-52}$ | 8.12589 |
수학적 풀이
uniform distribution을 따르는 random variable $X$의 확률밀도함수(probability density distribution, pdf)가 다음과 같을 때를 생각해 보자.
\begin{equation} f(x) = \begin{cases} 1, & \text{if $0 \le x \le 1$.} \newline 0, & \text{otherwise.} \end{cases} \end{equation}
\[\int_{-\infty}^{\infty} f(x) = 1\]그렇다면 다음이 성립한다.
\[P(a \le X \lt b) = \int_{a}^{b} f(x)dx\]random variable의 함수는 그 자체로 random variable이고 $y$가 어떠한 변환 함수 $y(X)$에서 나온다면, $Y = y(X)$는 X로부터 유도된 random variable이 된다. $X=a$일 때는 $Y=y(a)$, $X=b$일 때는 $Y=y(b)$인 식이다. 간단히 이해하기 쉽도록 $y$를 단조 증가함수라고 가정해 보면, $a \le X \lt b$라면 $y(a) \le Y \lt y(b)$일 것이고, 따라서 $P(a \le X \lt b) = P(y(a) \le Y \lt y(b))$일 것이다. 그러므로
\[P(y(a) \le Y \lt y(b)) = P(a \le X \lt b) = \int_{a}^{b} f(x)dx = \int_{y(a)}^{y(b)} f(x(y))\frac{dx}{dy}dy\]이고, $Y$의 pdf 를 $g(y)$라 하면
\[P(y(a) \le Y \lt y(b)) = \int_{y(a)}^{y(b)} f(x(y))\frac{dx}{dy}dx = \int_{y(a)}^{y(b)} g(y)dy\]즉 $g(y) = f(x)\frac{dx}{dy} = \frac{dx}{dy}$, 또는,
\[x = \int g(y)dy \Rightarrow x=G(y)\] \[y = G^{-1}(x)\]가 되어 $g(y)$인 pdf를 따르는 random variable $Y$를 uniform distribution을 따르는 $X$로부터 얻을 수 있는 것이다.
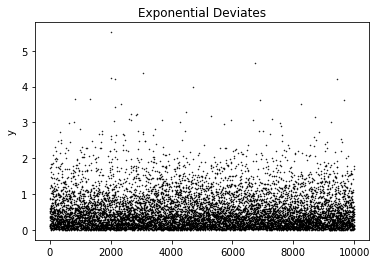
예시 - Exponential Deviates
pdf가 $f(y) = \lambda e^{-\lambda y}$ ($\lambda \gt 0$는 y의 평균값이다) 일 때, uniform random variable $X$로부터 $Y = y(X)$를 구해보자. 먼저 $F(y) = \int f(y)dy$를 구하면
\[F(y) = \int_{0}^{y} f(y)dy = 1-e^{-\lambda y} = x\]따라서
\[y(x) = F^{-1}(x) = -\frac{\ln(1-x)}{\lambda}\text{, or } -\frac{\ln(x)}{\lambda}\]로 uniform deviate $x$로부터 exponetial distribution을 따르는 $y$를 얻었다.
Lambda = 2.0
y = -np.log(uniform_sample)/Lambda
plt.figure()
plt.plot(y, marker='.', ls='', c='k', ms=1)
plt.title('Exponential Deviates')
plt.ylabel('y')
x = np.arange(np.min(y), np.max(y), 0.001)
fx = Lambda * np.exp(-Lambda*x)
plt.figure()
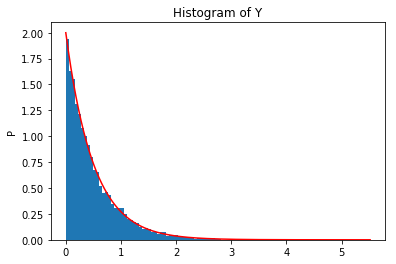
plt.hist(y, bins=100, density=True)
plt.plot(x, fx, c='r')
plt.title('Histogram of Y')
plt.ylabel('P')
문제점
위의 방법으로 원하는 확률분포를 따르는 난수를 생성하려면 해당 pdf를 적분해 누적확률분포(cumulative distribution function, cdf)를 얻어야 하고 이 cdf에 역함수를 구해야 한다. discrete한 확률분포의 경우 이는 컴퓨터로 계산하기 어렵지 않지만, pdf가 연속함수인 경우에는 해석적으로 적분이 안되는 경우가 많다. 이러한 경우 위의 uniform sample을 이용하는 방법에서 더 나아가 rejection sampling과 같은 방법을 쓴다고 한다(이 방법은 아직 알아보지 않아서 나중에…). 또한 Gaussian 분포의 경우 Box-Muller 방법을 사용해 두 개의 uniform random variable로부터 두 개의 random gaussian variable을 얻을 수 있다.

