박형욱 Hyeonuk Bahk

박형욱 Hyeonuk Bahk

Graduate student at SNU.
Astronomy major
studying extragalactic astronomy and observational cosmology.

Python Calculation of the Mass Functions from Press-Schechter Theory

3 minute read 

from pathlib import Path
import numpy as np
from astropy.table import Table
from astropy import units as u
from matplotlib import pyplot as plt
from tqdm import trange
import camb
from camb import model
from astropy import constants as c

plt.rcParams['font.size'] = 16
plt.rcParams['axes.labelsize'] = 20

WD = Path.home() / 'notebook' / 'cosmology' / 'mass_ftn'

# Make the matter power spectrum using CAMB

npoints = 3000

# MDPL2 cosmology
As_init = 2.1073e-9
h = 0.677
omb = 0.048
om = 0.31

ombh2 = omb * h**2
omch2 = (om-omb) * h**2
pars = camb.CAMBparams()
pars.set_cosmology(H0=100*h, ombh2=ombh2, omch2=omch2)
pars.InitPower.set_params(ns=0.96, As=As_init)
#Note non-linear corrections couples to smaller scales than you want
pars.set_matter_power(redshifts=[0.], kmax=2.0)

#Linear spectra
pars.NonLinear = model.NonLinear_none
results = camb.get_results(pars)
kh0, z0, pk0 = results.get_matter_power_spectrum(minkh=1e-4, maxkh=10,
                                              npoints=npoints)
s8 = np.array(results.get_sigma8())

# normalization with sigma8 = 0.8228
s8_ratio = 0.8228/s8[0]
As = s8_ratio**2 * As_init

pars = camb.CAMBparams()
pars.set_cosmology(H0=100*h, ombh2=ombh2, omch2=omch2)
pars.InitPower.set_params(ns=0.96, As=As)
pars.set_matter_power(redshifts=[0.], kmax=2.0)
pars.NonLinear = model.NonLinear_none
results = camb.get_results(pars)
kh, z, pk = results.get_matter_power_spectrum(minkh=1e-4, maxkh=10,
                                              npoints=npoints)
kh8 = 2*np.pi / 8

fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111)
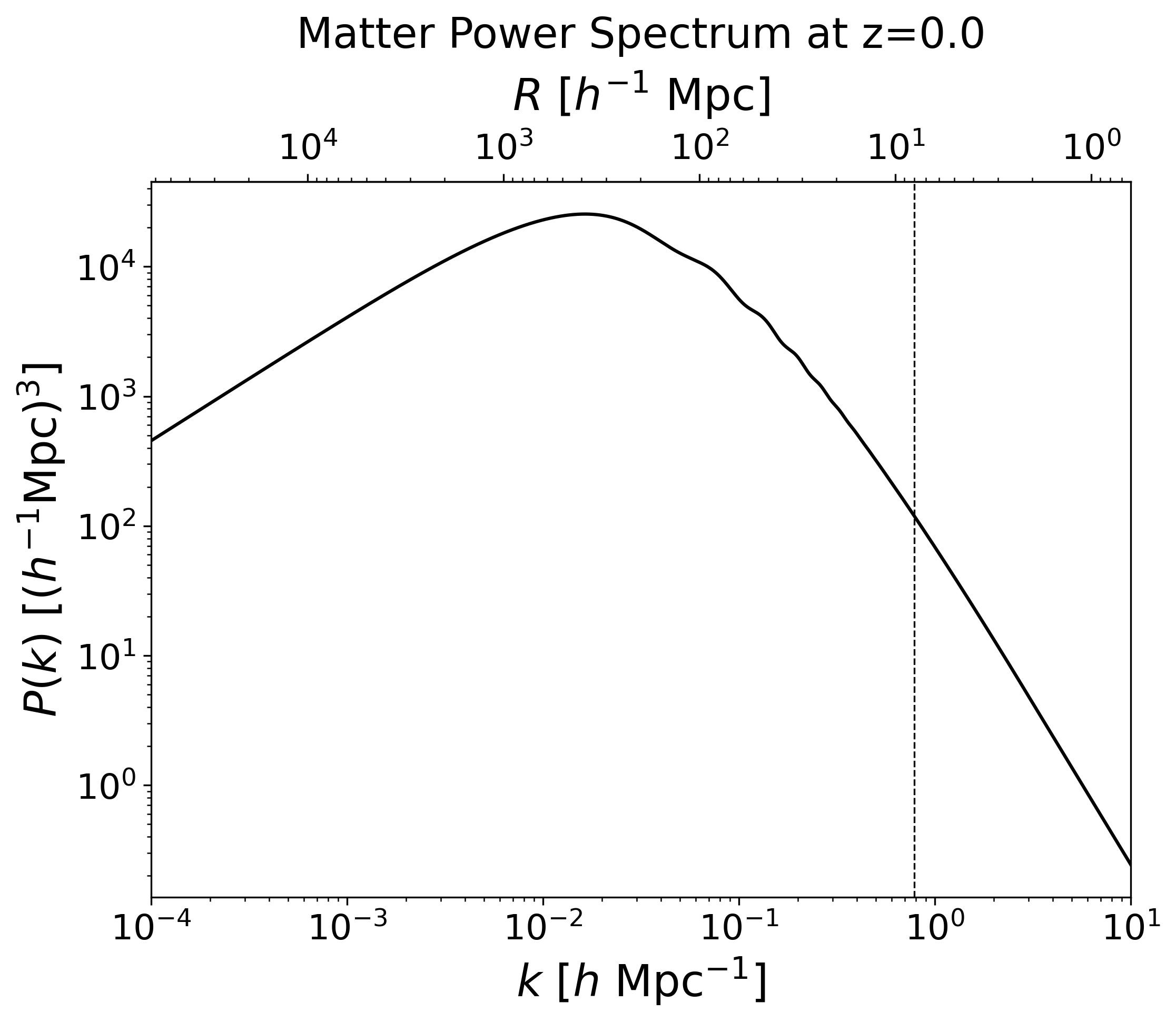
ax.loglog(kh, pk[0,:], color='k')
ax.set_ylabel(r'$P(k)$ [$ (h^{-1} {\rm Mpc})^3 $]')
ax.set_xlabel(r'$k$ [$h$ Mpc$^{-1}$]')
ax.axvline(kh8, c='k', lw=0.8, ls='--')
ax.set_xlim(1e-4, 1e1)
secax = ax.secondary_xaxis('top', functions=(lambda x: 2*np.pi/x, lambda x: 1/x/(2*np.pi)))
secax.set_xlabel(r'$R$ [$h^{-1}$ Mpc]', labelpad=10)
ax.set_title(f'Matter Power Spectrum at z={z[0]}', pad=10)
fig.savefig(WD/f'power_spectrum_z{z[0]}.png', dpi=300, bbox_inches='tight')

png

http://www.astro.yale.edu/vdbosch/astro610_lecture9.pdf

The Press-Schechter mass function with normalization factor of 2,

\[n(M,t)dM = \frac{dN}{dM}dM = \frac{1}{M}\frac{dN}{d\ln M}dM\] \[n(M,t)dM = \frac{\bar{\rho}}{M} \frac{\partial F(>M)}{\partial M}dM = 2\frac{\bar{\rho}}{M} \frac{\partial \mathcal{P}(> \delta_c)}{\partial M}dM\] \[\frac{dN}{d\ln M} = \sqrt{\frac{2}{\pi}}\frac{\bar{\rho}}{M}\frac{\delta_c}{\sigma_M} \exp \left(-\frac{\delta_c^2}{2\sigma^2_M}\right)\left|\frac{d\ln \sigma_M}{d \ln M}\right|\]

Defining the variable $\nu \equiv \delta_c(t)/\sigma(M)$,

\[\frac{dN}{d \ln M} = \frac{\bar{\rho}}{M}f_{\rm PS}(\nu)\left|\frac{d \ln \nu}{d \ln M}\right|\]

where

\[f_{\rm PS}(\nu) = \sqrt{\frac{2}{\pi}}\nu e^{-\nu^2/2},\]

which called the muliplicity function.

Sheth-Tormen mass function

\[f(\sigma) = A\sqrt{\frac{2a}{\pi}}\left[1+\left(\frac{\sigma^2}{a\delta_c^2}\right)^P\right]\exp\left(-\frac{a}{2}\frac{\delta_c^2}{\sigma^2}\right)\]

Jenkins mass function

\[f(\sigma) = 0.315 \exp[-|\ln \sigma^{-1} +0.61|^{3.8}]\] 
# filter definitions
def tophat(k, r_f):
    num = np.sin(k*r_f) - k*r_f*np.cos(k*r_f)
    den = (k*r_f)**3
    return 3 * num / den

def gaussian(k, r_f):
    return np.exp(-(k*r_f)**2 * 0.5)

def sharp_k(k, r_f):
    _thres = 1 / r_f
    _filter = np.ones_like(k)
    _filter[k > _thres] = 0
    return _filter

def sig_squared(filt, k, pk, r_f):
    kk = k[:, np.newaxis]
    pp = pk[:, np.newaxis]
    rr = r_f[np.newaxis, :]
    integrand = kk**2 * pp * filt(kk, rr)**2 / np.pi**2 / 2.
    return np.trapz(integrand, k, axis=0)

def mass_to_r(mass, h, filt='tophat'):
    _rho = om*2.7754e11 * u.Msun / u.Mpc**3
    
    gam_f = {'tophat': 4*np.pi/3,
             'gaussian': (2*np.pi)**(3/2),
             'sharp_k': 6*np.pi**2}
    
    r3 = mass / _rho / gam_f[filt]
        
    return r3**(1/3)

def r_to_mass(r, filt='tophat'):
    _rho = om*2.7754e11 * u.Msun / u.Mpc**3
    gam_f = {'tophat': 4*np.pi/3,
             'gaussian': (2*np.pi)**(3/2),
             'sharp_k': 6*np.pi**2}
    
    return _rho * gam_f[filt] * r**3

r_f = np.linspace(1, 64, 1000)*u.Mpc
mass = r_to_mass(r_f, filt='tophat')
rho_mean = om*(3*(100*u.km/u.s/u.Mpc)**2/(8*np.pi*c.G)).to(u.Msun*u.Mpc**(-3))
delt_c = 3/5*(3/4)**(2/3)*(2*np.pi)**(2/3)
sig2 = sig_squared(tophat, kh, pk[0,:], r_f.value)
sig = np.sqrt(sig2)

# Press-Schechter mass function
dlnsig = np.gradient(np.log(sig))
dlnM = np.gradient(np.log(mass.value))
multi_func_PS = np.sqrt(2/np.pi) * delt_c/sig * np.exp(-0.5*delt_c**2/sig2)
dNdlnM_PS = multi_func_PS * rho_mean/mass * np.abs(dlnsig/dlnM)

# Sheth-Tormen mass function
AA = 0.3222
aa = 0.707
PP = 0.3
nu = delt_c/sig
multi_func_ST = AA*np.sqrt(2*aa/np.pi)*(1+(1/aa/nu**2)**PP)*nu*np.exp(-aa/2*nu**2)

dNdlnM_ST = multi_func_ST * rho_mean/mass * np.abs(dlnsig/dlnM)

# Jenkins mass function
multi_func_Jenkins = 0.315*np.exp(-np.abs(np.log(1/sig)+0.61)**3.8)
dNdlnM_Jenkins = multi_func_Jenkins * rho_mean/mass * np.abs(dlnsig/dlnM)

fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(111)
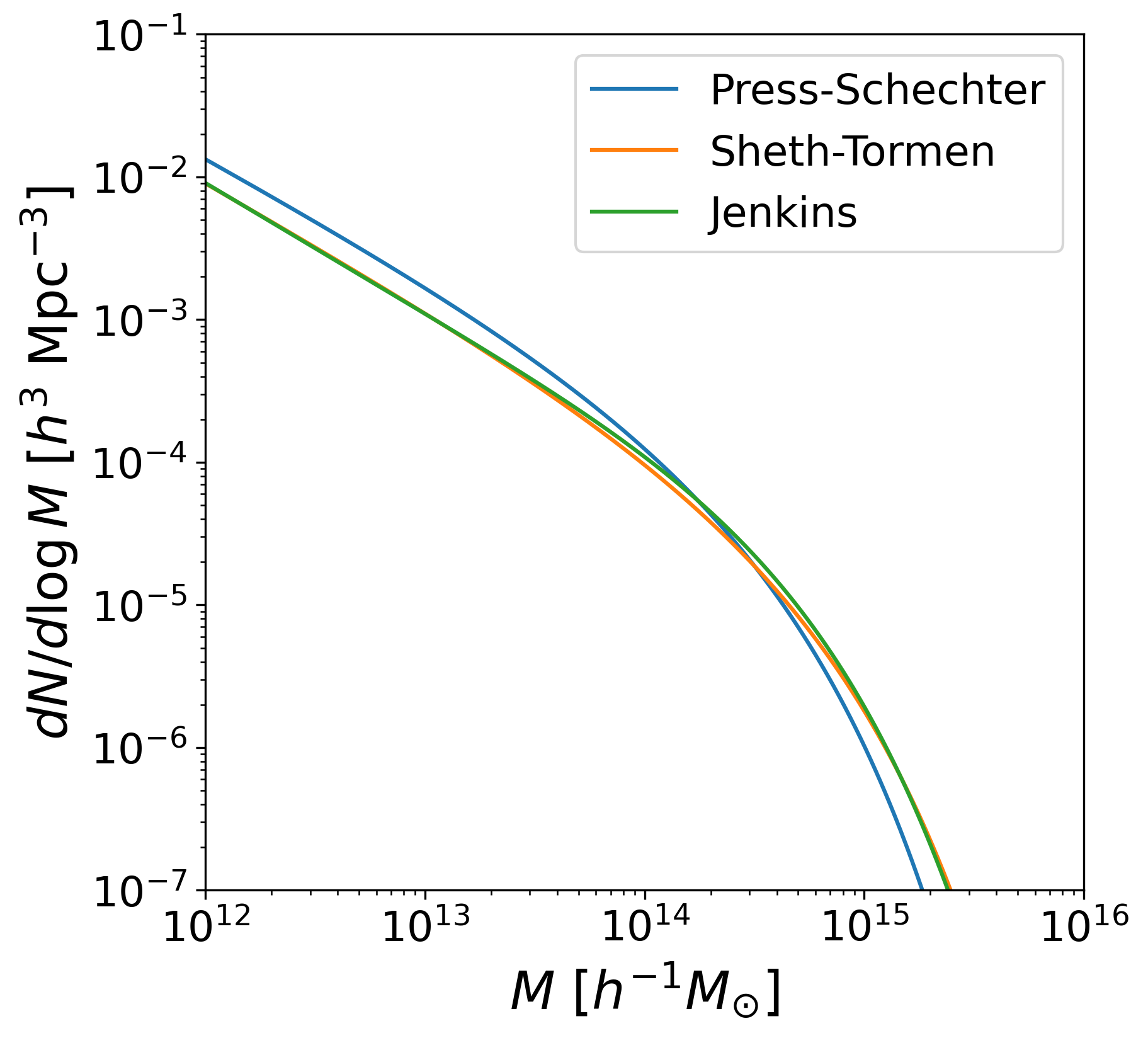
plt.plot(mass, np.log(10)*dNdlnM_PS, label='Press-Schechter')
plt.plot(mass, np.log(10)*dNdlnM_ST, label='Sheth-Tormen')
plt.plot(mass, np.log(10)*dNdlnM_Jenkins, label='Jenkins')
ax.set_xscale('log')
ax.set_yscale('log')
ax.set_xlim(1e12, 1e16)
ax.set_ylim(1e-7, 1e-1)
ax.set_xlabel('$M$ $[h^{-1} M_{\odot}]$')
ax.set_ylabel('$dN/d\log M$ [$h^{3}$ Mpc$^{-3}$]')
ax.legend()
fig.savefig(WD/'mass_ftn_theory.png', dpi=300, bbox_inches='tight')

png

# Mass function from MDPL2 rockstar catalog
rstpath = WD / 'data' / 'mass_rockstar.csv'
rst = Table.read(rstpath, format='ascii.csv', guess=False,
           fast_reader={'chunk_size': 100 * 1000000})
mrst = rst['mass'].data

# Bootstrapping to estimate the error
N_BOOTSTRAP = 1000
np.random.seed(100)
bins = np.linspace(np.log(1e12),np.log(1e15),21)

mass_sim = mrst

boot_rst = np.empty((N_BOOTSTRAP, len(bins)-1))

for i in trange(N_BOOTSTRAP):
    m = np.random.choice(mass_sim, len(mass_sim))    # a bootstrap resample
    logm = np.log(m)
    dn, binedgs = np.histogram(logm, bins)
    dlnm = np.diff(bins)
    boot_rst[i] = dn/dlnm/1e9    # per unit volume (total size: 1 Gpc)

n_mean_rst = np.mean(boot_rst, axis=0)
n_med_rst = np.median(boot_rst, axis=0)
N_data_rst, _ = np.histogram(np.log(mrst), bins)
n_data_rst = N_data_rst/dlnm/1e9
n_err_rst = np.std(boot_rst, axis=0)

btab_rst = Table({'n_mean': n_mean_rst, 'n_med': n_med_rst,
                  'n_data': n_data_rst, 'n_err': n_err_rst})
btab_rst.write(WD/'data'/'rst_mftn.csv', format='ascii.csv', overwrite=True)

x = 0.5*(bins[1:] + bins[:-1])
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(111)
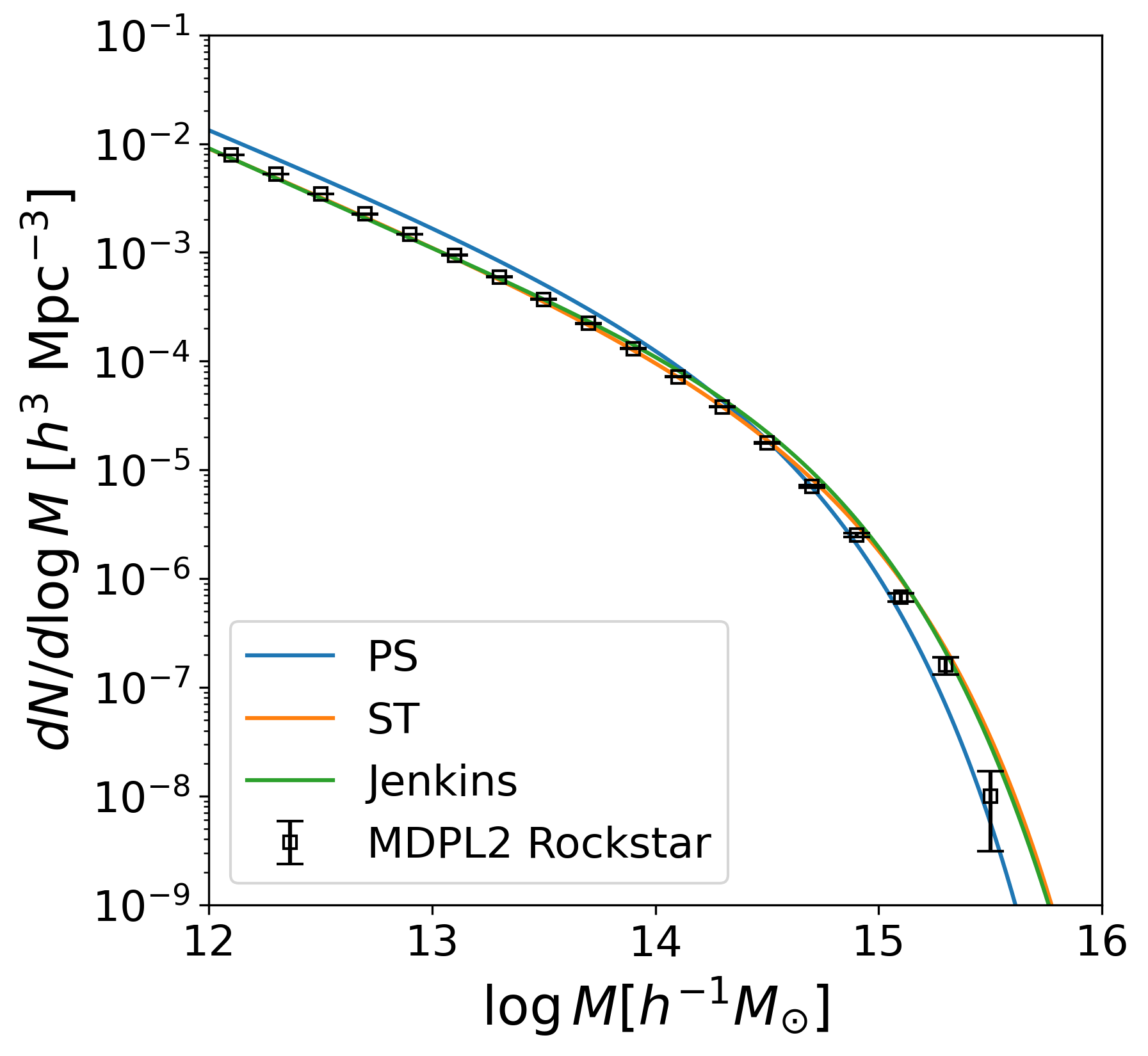
ax.plot(np.log10(mass/u.Msun), np.log(10)*dNdlnM_PS, label='PS')
ax.plot(np.log10(mass/u.Msun), np.log(10)*dNdlnM_ST, label='ST')
ax.plot(np.log10(mass/u.Msun), np.log(10)*dNdlnM_Jenkins, label='Jenkins')

ax.errorbar(x/np.log(10), np.log(10)*n_data_rst, np.log(10)*n_err_rst,
            c='k', capsize=5, ls='none', ms=5,
            marker='s', mfc='none', label='MDPL2 Rockstar')
ax.set_yscale('log')
ax.set_xlabel('$\log M [h^{-1} M_{\odot}]$')
ax.set_ylabel('$dN/d\log M$ [$h^{3}$ Mpc$^{-3}$]')
ax.legend()
ax.set_xlim(12, 16)
ax.set_ylim(1e-9, 1e-1)
fig.savefig(WD/'mass_ftn.png', dpi=300, bbox_inches='tight')

png

You may also enjoy

Great Sentenses 2

less than 1 minute read

Each one of us here today will at one time in our lives look upon a loved one who is in need and ask the same question: We are willing to help, Lord, but ...

Great Sentenses 1

less than 1 minute read

In the paradigm of lambda cold dark matter (ΛCDM), the majority of the matter density of the universe does not couple to electromagnetic fields, leaving i...